Diffraction
In the VCE curriculum, single slit diffraction remains one of the topics that scores poorly. Of particular concern is the number of students who, when asked to relate the observation of diffraction to certain wavelength:slit width ratios, make erroneous statements.
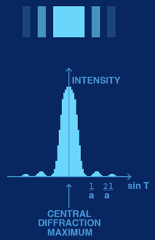

The single slit diffraction pattern is characterised by a central bright maximum which dims to (nearly) zero as you move away from the centre of the pattern in either direction before brightening slightly in a series of small side lobes. The central maximum is wider and brighter than the side lobes. When we refer to the width of the pattern, we are referring to the width of the central maximum
Deriving the wavelength : slit ratio
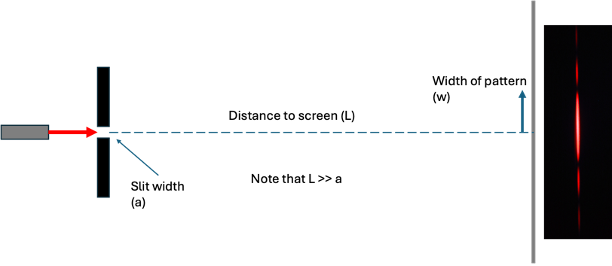
We begin by considering three rays from either end of the slit and the middle of the slit heading towards the screen.
In reality, they converge but because the ratio the distance to the screen is many orders of magnitude greater than the width of the slit, we can draw them as parallel.
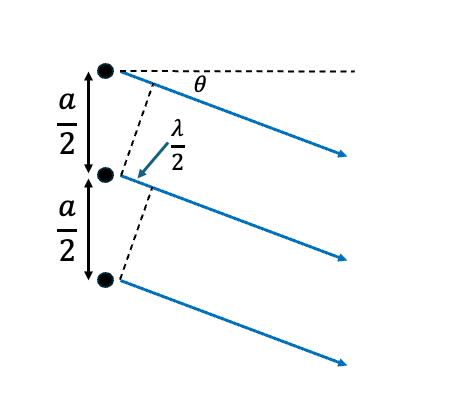
Now, we consider the three rays leaving at an angle, theta, such that they all converge at the edge of the central maximum. To result in a region of destructive interference, each ray must arrive 180˚ degrees out of phase with the previous ray. That is, ray 2 is out of phase with ray 1 and ray 3 is out of phase with ray 2.
From here we can identify two similar triangles.
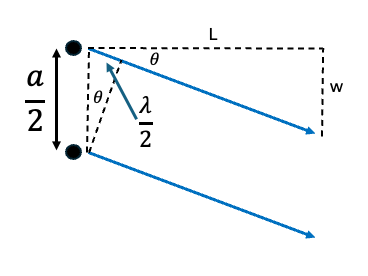
and
Since L >> w, theta is very, very small and for small theta we can use the approximation:
and equate the two side. This will simplify to
The resultant conclusion is the one that students refer to when they state that if slit width and wavelength are equal then diffraction is greatest. The problem here is that "greatest" is not defined and if students are asked to explain further they have nothing to add.
Quantification with sine
Students may go back to the derivation and appeal to the formula:
Students state that if a >> wavelength then:
Which tends to a very small angle and the width of the pattern is very small. If the width if very small then the pattern looks like a dot and no diffraction can be seen.
if a and wavelength are similar then
The implication of this 90˚ needs to be stated. The pattern will be:
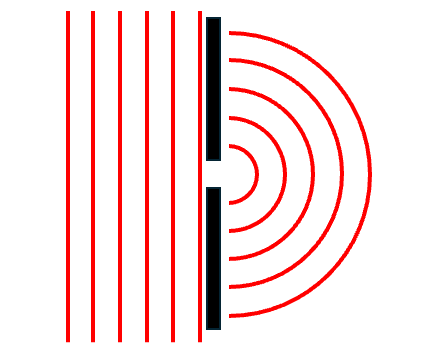
One could argue that it is not possible to observe the diffraction pattern since there is only a uniform spread of light and the edges of the pattern cannot be seen. We will put that arguement to one side.
Students run into a problem when the slit width is less than the wavelength. In this case they find themselves typing something like:
into their calculator and getting an error. At this point they either state that diffraction cannot be observed or they hedge and say "diffraction will occur but will not be obvious." in an attempt to shore up a mark for yes and a mark for no. They actually get no marks because they do not know the answer.
Fraunhoffer equation
The correct equation to visualise the intensity of the pattern with respect to angle of spread is:
This can be written as
The patterns
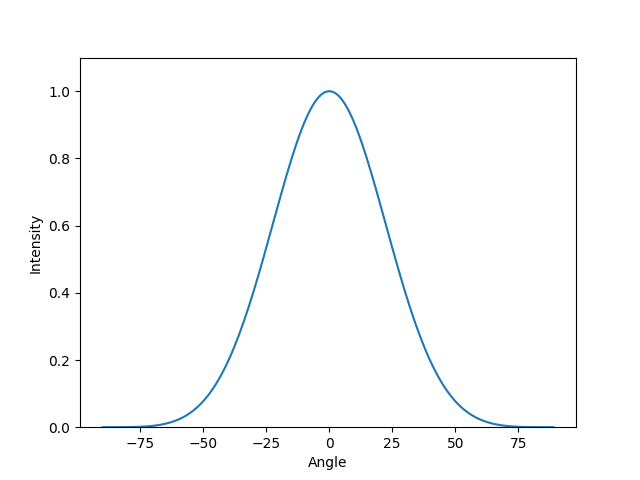
Lambda = a
If the slit width and lambda are equal then the pattern will look like the one below. Note that the pattern is quite wide, not dimming below 20% until around the 50˚ mark
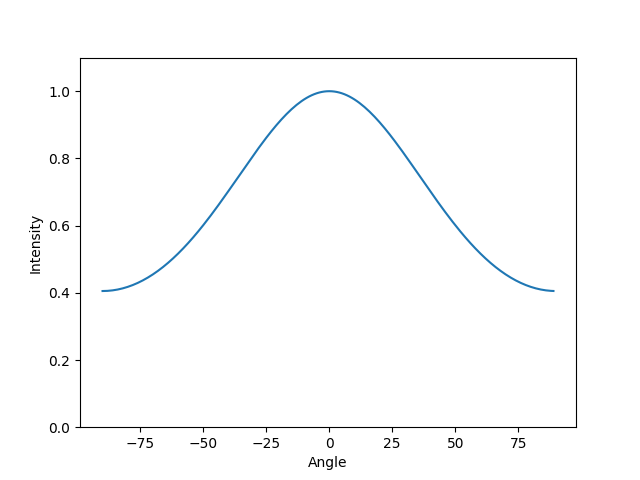
Lambda = 2a
If lambda doubles to twice the slit width then the pattern widens significantly. Note that the decrease in intensity is greatly reduced compared to the previous example. At ~50˚ the intensity is still greater than 50%.
Lambda = 10a
if lambda is much, much greater than the slit width then the brightness is equally spread across all angles and it is difficult to observe any change in intensity.
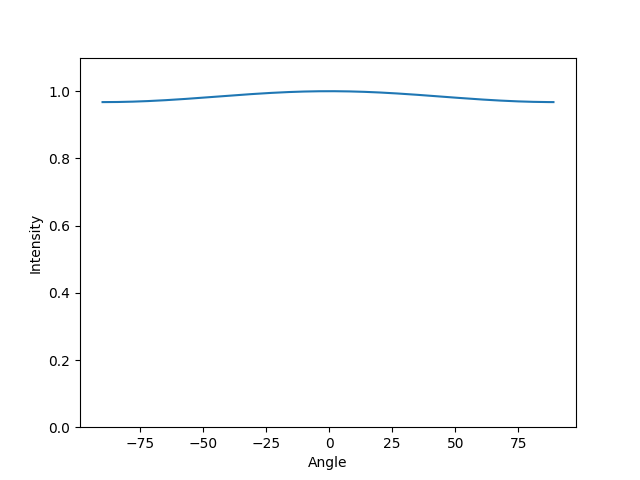
Lambda = a/2
This time we test if the wavelength is half the slit width. Not only is the cental maximun vissible but so too are the side lobes with their lower intensity.
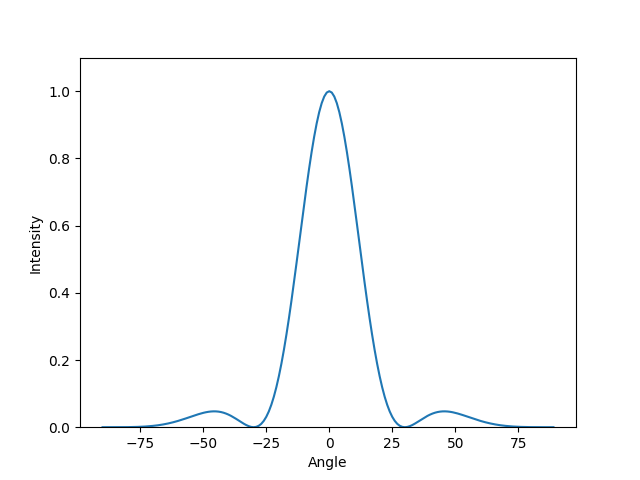
Lambda = a/10
As the wavelength gets very small compared to the slit width, the pattern continues to narrow.
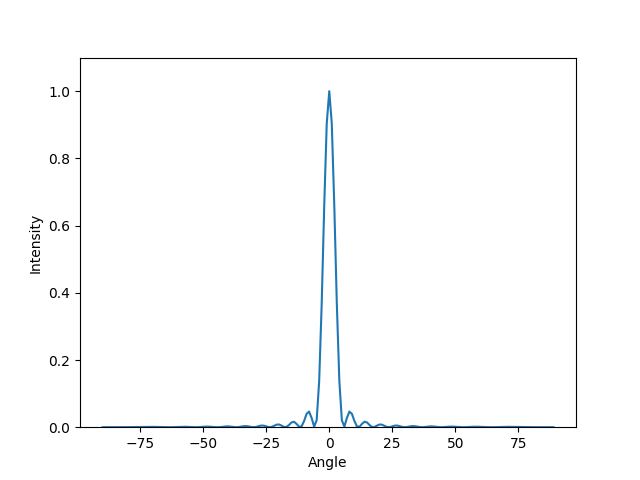
Summary
If observable diffraction is the spreading of the light beam then it can be seen where the ratio of λ/a ranges from 0.1 up to (and beyond) 10. If the wavelength is one hundred times the slit width then the intensity is evenly spread across all angles. The edge of the pattern cannot be discerned but the effect certainly can be.
If the slit width is one hundred times the wavelength then there is no discernable spread and the light appears as a dot.