The IEEE 574 standard

Basic binary

This will be kept short since anyone reading this already know about binary numbers.

Suffice to say that if we consider a 32 bit binary number, the most basic conversion of 32 1's to decimial gives 4,294,967,295 and that's without negative numbers or decimals. IEEE 574 allows values from -3.4 x10³⁴ up to 3.4 x10³⁴. The process is really interesting.

Float 32 structure

The way the 32 bits are used to create a floating point number is shown below.

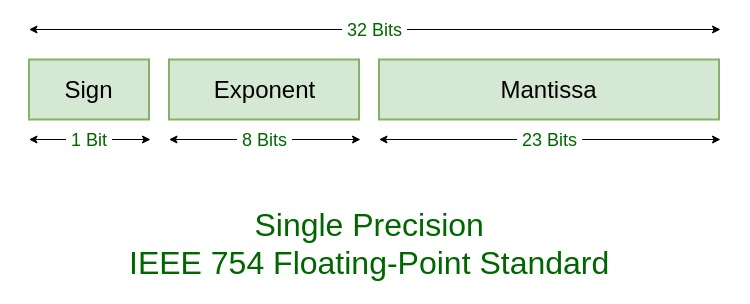
Bit 31 is used for the sign. Zero is a positive number and one is a negative number.

Bits 23 to 30 (8 bits) are used for the exponent. The exponent uses an excess 127 calculation. The implementation of this will be shown in the examples below

Bits 0 to 22 are the mantissa and hold the actual number. There is an assumed "1" at the beginning of the number that is not stored in the value. This means that if the value to be stored was 1011.110 it would be stored as 011110 with the leading "1" omitted.

Example 1

Convert 487.37350 to a 32 bit representation

Step 1. Convert 487 to binary

487 in binary is 1 1110 0111

Step 2. Convert 0.37350 to binary

There are twenty-three bits in the mantissa so there will be fifteen decimal places after the initial eight bits. Each of these bits refers to fractions that add as closely to 0.37350 without going over.

Or, if you prefer:

Not each fraction is used and binary notation is used to confirm which fractions are used and which are not.

The bit pattern required to get as close to 0.37350 without going over is 010 1111 1100 1110 and gives a value of 0.37347412109375.

You can see there is a small conversion error. 487.37350 is going to be stored in memory as 487.37347412109375

Step 3. Initial binary representation

At this point the binary representation of the floating point value is 1 1110 0111.0101 1111 1001 110. This needs to be converted to "scientific notation", that is 1.1110 etc. The current value of 1 1110 0111.0101 1111 1001 110 can be represented as 1.1110 0111 0101 1111 1001 110 x 2⁸.

Step 4. Determine the exponent

The exponent is calculated using the excess 127 method. This means the current exponent (8) is added to 127.

These become bits 30 down to 23

Step 5. Construct the final representataion

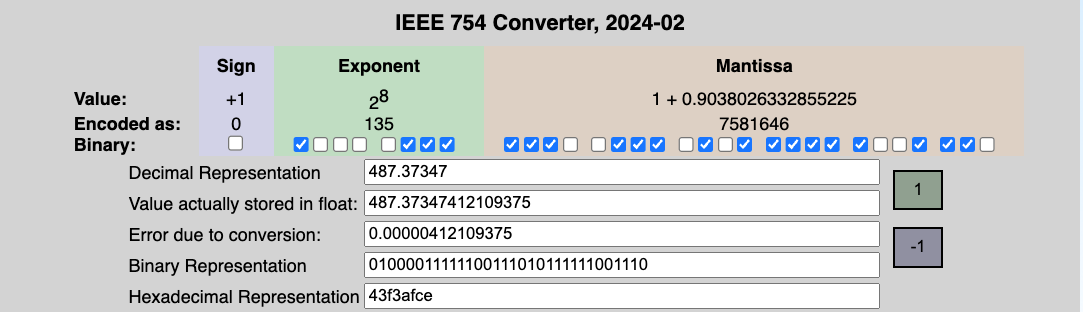
The number is positive so bit 31 will be 0. The exponent is 135 so bits 23 to 30 will be 1000 0111 The value is 1.1110 0111 0101 1111 1001 110 The leading zero is dropped and bits 22 to 0 are 1110 0111 0101 1111 1001 110 The final value in memory is 0 1000 0111 1110 0111 0101 1111 1001 110

Internet check This site: https://www.h-schmidt.net/FloatConverter/IEEE754.html is a great way to check your understanding. Putting the above result in using the check boxes gives:

Example 2

Convert Newton's gravitational constant to float32

Newton's gravitational constant is 6.67430 x 10^-11

Step 1. The fractional part

There is no whole part so move straight on to the fractional part. In decimal notation the number is 0.0000000000667430

The table above can be used to find the binary representation of this value. It has to be extended beyond its fifteen bit limit. The process needs to continue until there are 23 'significant' bits. The final representation is:

000000000000000000000000000000000100100101100010011110111

Step 2. Convert to scientific notation

The above value can be represented as : 1.00100101100010011110111 x 2^-34.

Step 3. Determine the exponent

Using the excess 127 method: 127 + (-34) = 93 The exponent = 0101 1101

Step 4. Construct the final value

The number is positive so bit 31 will be 0. The exponent is 93 so bits 23 to 30 will be 0101 1101 The value is 1.00100101100010011110111 The leading zero is dropped and bits 22 to 0 are 0010 0101 1000 1001 1110 111 The final value in memory is 0 0101 1101 0010 0101 1000 1001 1110 111

Internet check