Aitkin

The Sieve of Aitkin is a modern sieve based on number theory rather than brute force. In the absence of a more definative guide I will use the wikipaedia page for the explanation of the steps. I'm also going to code this with the intent of demonstrating the process, not writing the most efficient code. We'll do that once we know how the sieve works.

We start with a dictionary with the keys being the prime candidates (sequential numbers) with all the values set to "not prime". We assume that all numbers are composite until proven otherwise. Because a single line dictionary output from Python is going to be hard to read (100 key:value pairs all looking like: 2:False, 3:False) so I'm going to use the grid below. Our first step is to mark 2, 3 and 5 as prime.

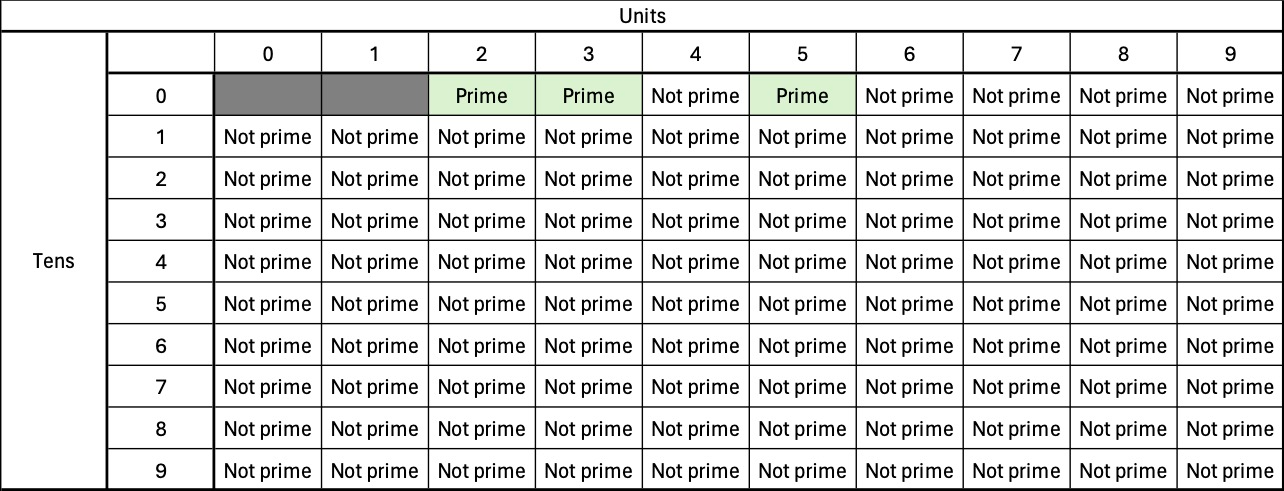
The first step is to find the modulo 60 remainder for each number in the sieve. We want the numbers for which the modulo 60 remainder is 1, 13, 17, 29, 37, 41, 49, or 53. These numbers are: [13, 17, 29, 37, 41, 49, 53, 61, 73, 77, 89, 97] We are to flip the status of the number from "not prime" to "prime" (and back again) for each solution to:

E.g. For the number "13":

This is the only solution that gives 13 so we flip 13 from not prime to prime.

17 only has one solution, 2 & 1, 29 only has one solution, 1 & 5, 37 only has one solution, 3 & 1 ... In fact, all the number in the list above only have one solution except 77 which has no solutions so all except 77 get marked as prime. This is good since 77 is not prime anyway.

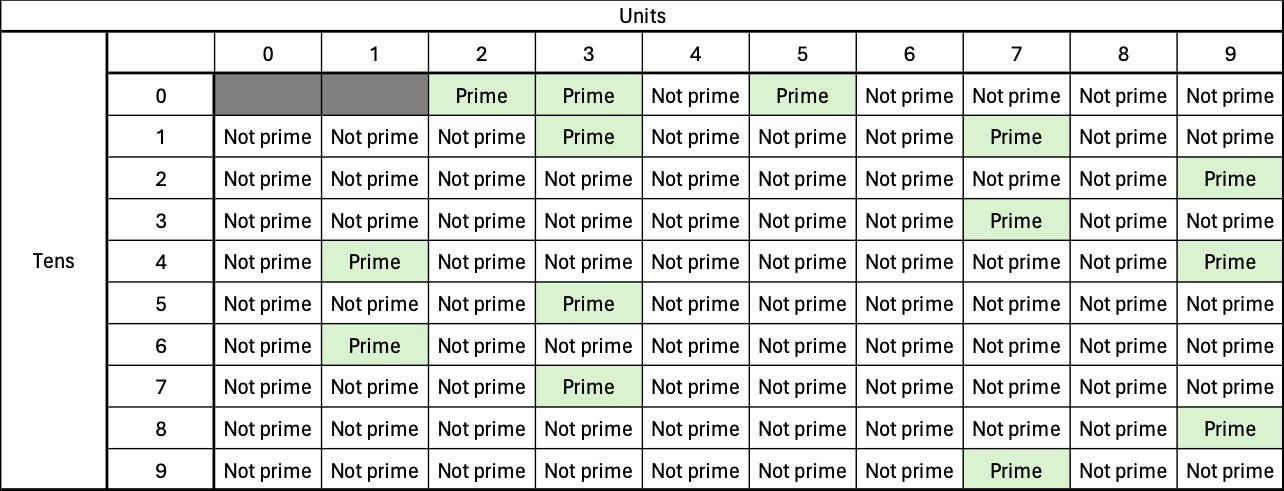
The second step is to find numbers with a modulo 60 remainder of N. These numbers are: [7, 19, 31, 43, 67, 79, 91] We are to flip the status of the number for each solution to:

All of the numbers have one solution except 91 which has two solutions; 3 & 8 and 5 & 4.

This means that we flip 91 from "not prime" to "prime" then back again so it will remain marked as not prime, which is good, because it isn't. The rest are prime so our grid now looks like this:

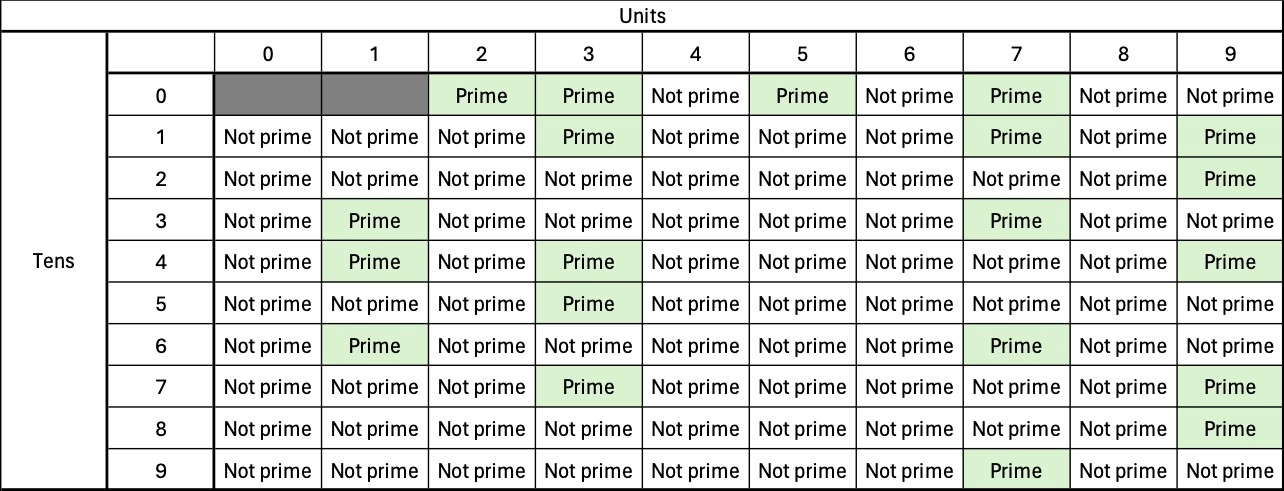
The third step is to find numbers with a modulo 60 remainder of 11, 23, 47, or 59. These numbers are [11, 23, 47, 59, 71, 83] We are to flip the status of the number for each solution to:

But only where x > y. All the numbers have only one solution that matches both criteria so they are all flipped to prime.

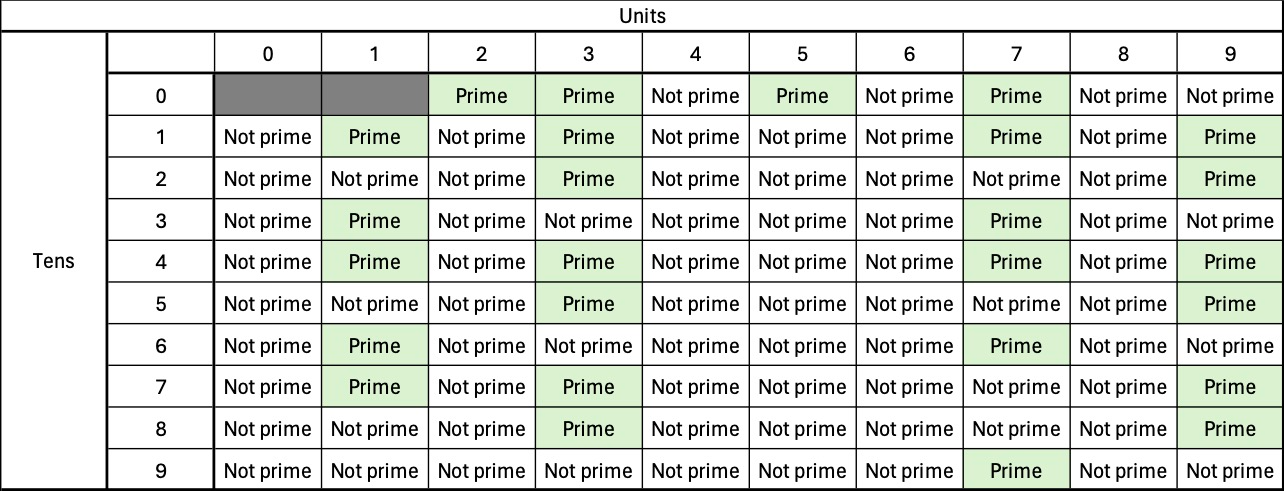
The final step is to check for any squares that might have snuck through so we look for multiples of 2 squared (4), 3 squared (9), 5 squared (25) and 7 squared (49). There won't be any squares of primes higher than this as our limit was 100. As it happens, 49 has snuck through so we reset it back to not prime.

And that's the job done. The final grid looks like this:

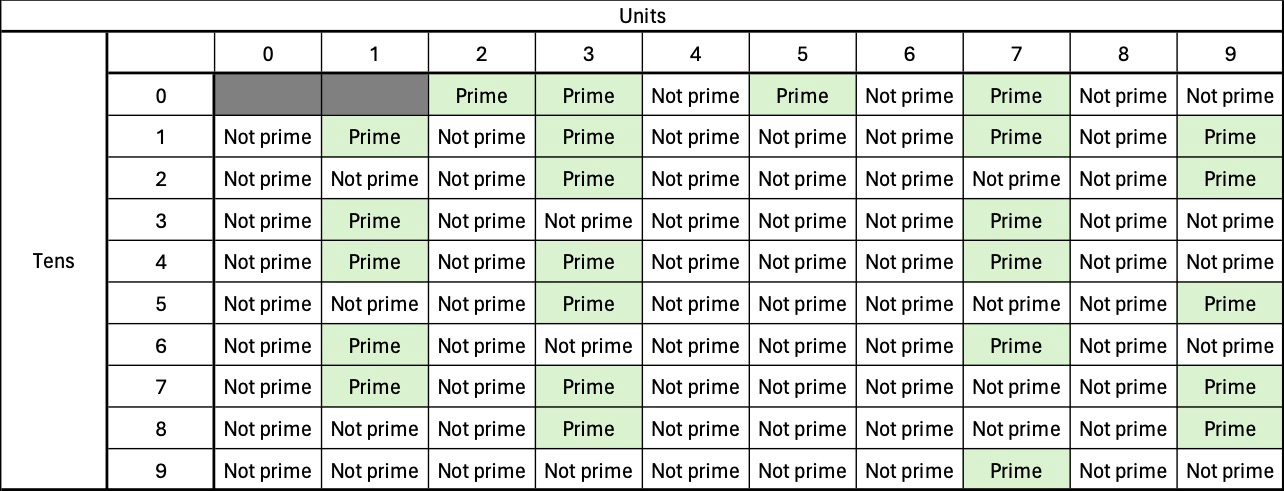
It now contains only primes.

Python code - First iteration

The most straight-forward implementation of the Aitkin sieve as it is described would look like this:

import time

start = time.perf_counter()
limit = 1_000
primes = [2, 3, 5]
sieve = {i:False for i in range(2, limit)}

case1 = [1, 13, 17, 29, 37, 41, 49, 53]
case2 = [7, 19, 31, 43]
case3 = [11, 23, 47, 59]

processing = time.perf_counter()
print(f'Setup time: {processing - start}')
for k,v in sieve.items():
    rem = k % 60
    if rem in case1:
        for x in range(1, int(limit**0.5)):
            for y in range(1, int(limit**0.5)):
                if (4 * x ** 2) + (y ** 2) == k:
                    sieve[k] = not sieve[k]
    if rem in case2:
        for x in range(1, int(limit**0.5)):
            for y in range(1, int(limit**0.5)):
                if (3 * x ** 2) + (y ** 2) == k:
                    sieve[k] = not sieve[k]
    if rem in case3:
        for x in range(1, int(limit**0.5)):
            for y in range(1, int(limit**0.5)):
                if (x > y) and ((3 * x ** 2) - (y ** 2) == k):
                    sieve[k] = not sieve[k]

for candidate,status in sieve.items():
    if status:
        primes.append(candidate)

print(primes)
stop = time.perf_counter()

print(f'Processing time: {stop - processing}')
print(f'Total time: {stop - start}')

First iteration - Time requirements

This version of the sieve is VERY slow. The Sieve of Eratosthenes can sieve to 100,000 in 0.02 sec. Trial division takes 0.17 sec to sieve 100,000 values, around 8.5 times slower. This incarnation of the Sieve of Aitkin takes 220 sec to sieve though 100,000 values. That makes it over 1200 times slower than Trial Division and 11,000 times slower than Eratosthenes.

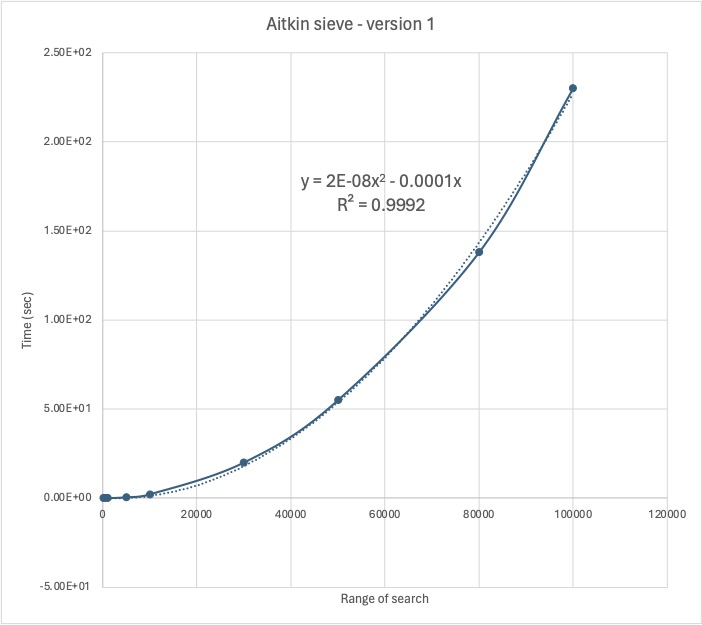
There has to be a better way to implement the Sieve of Aitkin.

First iteration - Space requirements

As we will see the bulk of the memory will be used to store the sieve dictionary. The memory breakdown is:

limit: 32 bytes
[primes]: 184 bytes initially and will grow to 4120 bytes
: 35824 bytes initially and will grow to 35856
[case1]: 376 bytes
[case2]: 216 bytes
[case3]: 216 bytes
k, v, rem, x & y: 32 bytes each

As can be seen, the memory requirements are driven by the size of the sieve dictionary which does not change size significantly. The remainder of the variables take 1184 bytes initially and will grow to 5120 once the prime list is filled.

Python code - Second iteration

In this iteration we will change the way we determine which values to check. Instead of looking up a list of remainers, we will implement the following:

Numbers with modulo 60 remainders of 1, 13, 17, 29, 37, 41, 49, or 53 will have a modulo 12 remainder of 1 or 5.
Numbers with modulo 60 remainder of 7, 19, 31, or 43 wil have a modulo 6 remainder of 1.
Numbers with modulo 60 remainder of 11, 23, 47, or 59 will have a modulo 12 remainder of 11.
Numbers that are perfect squares (sqrt(number) % 1 has no remainder) will be excluded.

We will also change the x and y loops to make them more efficient.

The equation:

Does not have to be tested for all value of x and y up to the square root of n. The largest value that y will take will occur when x = 1 and will have to be sqrt(n) but when y = 1, x only needs to go up to sqrt(N/4) so we can reduce the range on the loop.

A similar thing happens in the second loop where x only needs to increment until is equals sqrt(N/3).

The final loop is cannot be addressed in this manner as the y² term is subtracted not added. We can, however, apply the (x > y) requirement by setting the upper limit of the y loop to x.

Our code now looks like this:

import time
start = time.perf_counter()
primes = [2, 3, 5]
upper = 100000
for i in range(7, upper, 2): # Only worth checking odd numbers
    if ((i % 12 == 5) or (i % 12 == 1)) and ((i ** 0.5) % 1 != 0):
        for x in range(1, int((upper / 4) ** 0.5)):
            for y in range(1, int(upper ** 0.5), 2):
                if ((4 * x ** 2) + (y ** 2) == i):
                    if i not in primes:
                        primes.append(i)
                    else:
                        primes.remove(i)

    elif (i % 6 == 1) and ((i ** 0.5) % 1 != 0):
        for x in range(1, int((upper / 3) ** 0.5)):
            for y in range(1, int(upper ** 0.5)):
                if (3 * x ** 2) + (y ** 2) == i:
                    if i not in primes:
                        primes.append(i)
                    else:
                        primes.remove(i)

    elif (i % 12 == 11) and ((i ** 0.5) % 1 != 0):
        for x in range(1, int((upper / 2) ** 0.5)+1):
            for y in range(1, x):
                if ((3 * x ** 2) - (y ** 2) == i):  # Removed the (x > y) because the y for loop takes care of it.
                    if i not in primes:
                        primes.append(i)
                    else:
                        primes.remove(i)

for prime in primes:
    if prime < (upper ** 0.5):
        for i in range(prime**2, upper, prime**2):
            if i in primes:
                primes.remove(i)
                
print(len(primes))
stop = time.perf_counter()
print(stop - start)

Second iteration - Time requirements

This does speed up our code but not nearly enough. Compared to the original version it is about twice as fast.

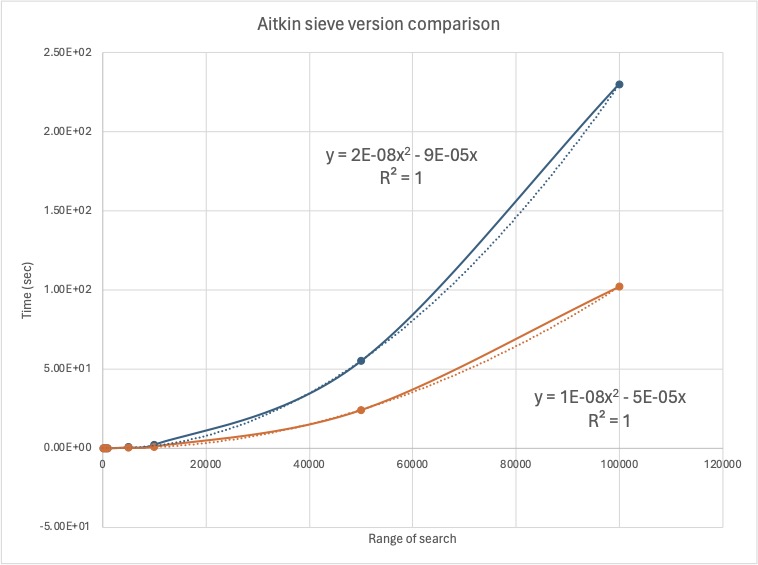
Second iteration - space requirements

This version runs in much less memory. The variables upper, i, x, & y all take 32 bytes each. The [primes] list starts at 184 bytes and rises to 4120 bytes when it contains 100 primes.

Python code - Third iteration

The previous two versions suffered from the repeated for loops for x and y. A different approach is to loop once through x and y and test the combinations.

This has its problems though. If x = 5 and y = 10 then 3x² + y² = 175 and this will be added to the primes list and will have to be removed after the initial sieve. The code now looks like this:

import time

start = time.perf_counter()
limit = 100
primes = [2, 3, 5]
lap_time = time.perf_counter()
for x in range(1, int(limit**0.5)+1):
    for y in range(1, int(limit**0.5)+1):
        n = (4 * x**2) + (y**2)
        if n <= limit and (n % 12 == 1 or n % 12 == 5) and ((n ** 0.5) % 1 != 0 ):
            if n not in primes:
                primes.append(n)
            else:
                primes.remove(n)

        n = (3 * x**2) + (y**2)
        if n <= limit and n % 12 == 7 and (n ** 0.5) % 1 != 0 :
            if n not in primes:
                primes.append(n)
            else:
                primes.remove(n)

        n = (3 * x**2) - (y**2)
        if x > y and n <= limit and n % 12 == 11 and ((n ** 0.5) % 1 != 0 ):
            if n not in primes:
                primes.append(n)
            else:
                primes.remove(n)

for prime in primes:
    if prime < (limit ** 0.5):
        for i in range(prime**2, limit, prime**2):
            if i in primes:
                primes.remove(i)

stop = time.perf_counter()
print(len(primes))

print(f'Setup time: {lap_time - start}, Processing time: {stop - lap_time}, Total time: {stop-start}.')

Third iteration - Time requirements

Again, this is much faster than previous attempts, but it is still very slow compared to trial division and Eratosthenes.

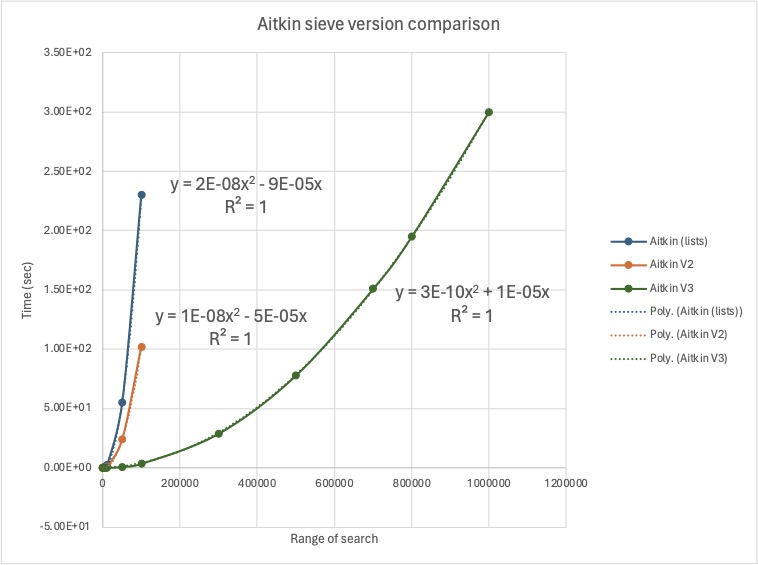
Third iteration - space requirements

The space requirements for this version are the same as for version 2. Most of the variables are 32 byte integers, while the [primes] list will start at 184 bytes and rise to 4120 bytes at the end.

Last modified: 25 May 2024