Eratosthenes

Introduction

The Sieve of Eratosthenes is a favourite of mine and I've been using it to teach Python lists for over a decade.

The algorithm is simple. Take a sequential list of numbers as prime candidates. The list can start at 2 since 1 is not considered to be a prime number.

[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ,13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]

Start at the bottom of the list. The number 2 is considered prime to leave it and cross off every 2nd number after it. I can't "cross off" numbers easily so I'll set them to zero.

[2, 3, 0, 5, 0, 7, 0, 9, 0, 11, 0, 13, 0, 15, 0, 17, 0, 19, 0, 21, 0, 23, 0, 25]

Now move up one place. The next value is 3, so it is prime and cross off every 3rd value after it.

[2, 3, 0, 5, 0, 7, 0, 0, 0, 11, 0, 13, 0, 0, 0, 17, 0, 19, 0, 0, 0, 23, 0, 25]

Now move up one place. That value is zero so move up one more place. The number 5 is prime so cross off every 5th number after it.

[2, 3, 0, 5, 0, 7, 0, 0, 0, 11, 0, 13, 0, 0, 0, 17, 0, 19, 0, 0, 0, 23, 0, 0]

The remaining values are all prime so we can end the demo here.

The upside for the Sieve of Eratosthenes is its simplicity and its speed. The downside is the memory requirements.

Alogrithm in pseudocode

[primes] = []
[numbers] <- sequential from 2 to upper_limit
for each number in [numbers]:
    If the number not 0:
        add number to [primes]
        step through [primes] for number in steps of number:
            set value to 0

The Python code:

import time

upper_limit = 1_000_000
start = time.perf_counter()
numbers = [x for x in range(2, upper_limit)]
setup_time = time.perf_counter()

primes = []
for i in range(len(numbers)):
    if numbers[i] != 0:
        primes.append(numbers[i])
        for j in range(i, len(numbers), numbers[i]):
            numbers[j] = 0

end = time.perf_counter()

print(len(primes))

print(f'Setup time: {setup_time - start}, Processing time: {end - setup_time}, Total time: {end - start}')

The setup time is more significant than the searching time. The set up time is 0.55 sec. The processing time is 0.20 sec and the total time to run is 0.75 sec.

Memory requirements

As with the trial division analysis, for the memory requirement we will reduce the upper limit to 542 which allows us to find the first 100 primes.

upper_limit: 32 bytes
primes: Initially 56 bytes and will grow
numbers: 22072 bytes
i: 32 bytes and while i will change, its size will not
j: 32 bytes and while i will change, its size will not

It is obvious that the integers are insignificant when compared to the two lists. The numbers list is initially 22 kB. We know that the list of [primes] will require 4,120 bytes once the run is completed. It would be easy to think that the total memory requirement for the app is ~26 kB but this is not the case.

The initial numbers list contains, 540 numbers. Initially this will require 56 bytes for the empty list and by the time it reaches 540 elements it will have enough memory reserved for 592 values. The reason for this can be seen in my pages on Python memory management. 56 Bytes + 592 x 8 bytes = 4792 bytes for the list object. There are 540 integers stored in the list requiring another 540 * 32 = 17280 bytes of memory. The total memory requirement for the initial numbers list is 4792 + 17280 = 22072 bytes.

After the first pass through the list, all the multiples of 2 have been set to zero. In this case all the pointers in the list will point to the same memory location. The size of the numbers list object will remain at 4792 bytes but there will only be 272 unique values. There are 271 integers greater than 0 and 269 integers equal to 0.

The memory required to store 272 integers is 272 * 32 = 8704 bytes. The memory required for the numbers list and its contents has fallen to 4792 + 8704 = 13,496 bytes.

The size of numbers will fall throughout the searching process. Initially the rate of reduction will be quite quick but it will trail off. By the end the two lists, numbers and primes, will be nearly the same size. The final sizes are 4824 bytes for the numbers list and 4120 bytes for the primes list. This is a total memory requirement of 8944 bytes.

Graphical analysis

If the memory use of Eratosthenes is graphed over time it looks like this:

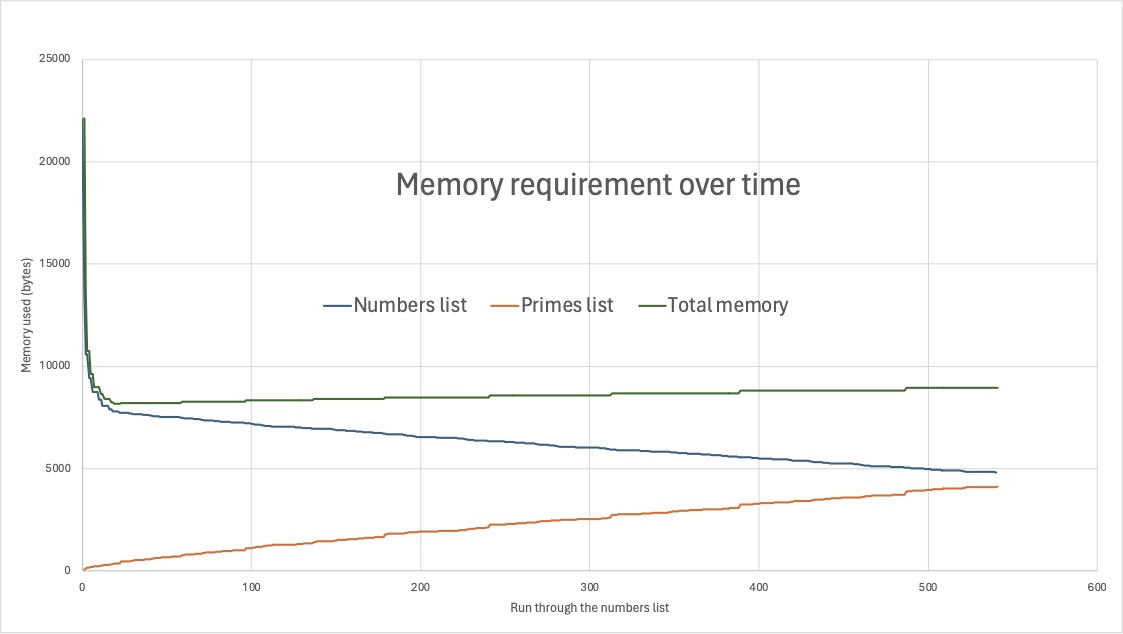
You can see that the initial memory usage is very high but drops quickly to less than half its original requirements and grows more slowly than the primes list over time due to the slow reduction in the size of the numbers list.

Time requirement

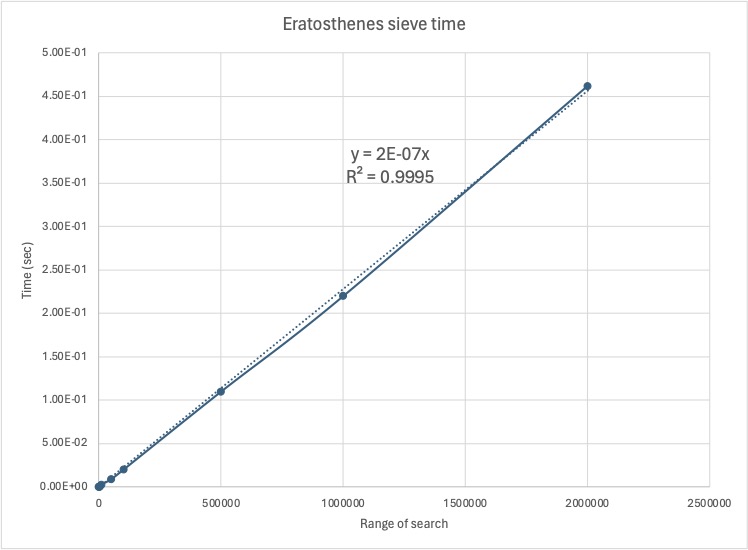
The Eratosthenes sieve runs in O(N) time as shown in the graph below:

Last modified: 25 May 2024