Trial division

Introduction

The trial division algorithm is predicated on all composite numbers having prime factors. For example:

4 has prime factor of 2
6 has prime factors of 2 and 3
8 has prime factor of 2
9 has prime factor of 3
10 has prime factors of 2 and 5

To speed up the algorithm we will only consider primes that are equal to or less than the square root of the number we are testing.

For example, the square root of 10 is 3.16. The integer value of this is 3. We only need to consider 2 and 3 as possible factors of 10 to determine if it is prime. Since 10 % 2 = 0, 10 is not prime, and we do not need to consider 5.

Consider 18. The square root is 4.246 or as an integer, 4. If neither 2 nor 3 are factors then 18 will be prime. Since both 2 and 3 are factors, 18 is not prime. Considering 19, the root is 4.358 or, again, 4 as an integer. If neither 2 nor 3 are factors then 19 will be prime. Since 19 % 2 = 1 and 19 % 3 = 1, 19 is prime.

25 is not prime because it has the prime factor of 5 but 27 is prime since neither 2, 3 nor 5 are factors

Algorithm in pseudocode

upper_limit <- 100  # This can be decided by the user
[primes] <- [2]
for test_value from 3 to upper_limit:
    root <- square_root(test_value)
    is_prime <- True
    for each value in [primes] less than root:
        if test_value % value == 0:
            is_prime <- False
    if is_prime = True:
        [primes] <- append test_value
        

Our initial python code is:

import time

upper_limit = 1_000_000
start = time.perf_counter()
primes = [2]
for i in range(3, upper_limit): # values to test
    root = int(i ** 0.5)  # from 0 to sqrt(value)
    prime_index = 0  # Start with first prime (2)
    is_prime = True  # Assume test value is prime
    while primes[prime_index] <= root:
        if i % primes[prime_index] == 0:
            is_prime = False   
        prime_index += 1
    if is_prime:
        primes.append(i)
end = time.perf_counter()

print(len(primes))
print( f'Processing time: {end - start}')

When tested, this had a processing time between 10 and 11 sec. This can be sped up by realising that the while loop does not need to complete. Once a prime results in is_prime being set to false we can terminate the search, so we will add a "break" after that line. The new code is:

import time

upper_limit = 1_000_000
start = time.perf_counter()
primes = [2]
for i in range(3, upper_limit): # values to test
    root = int(i ** 0.5)  # from 0 to sqrt(value)
    prime_index = 0  # Start with first prime (2)
    is_prime = True  # Assume test value is prime
    while primes[prime_index] <= root:
        if i % primes[prime_index] == 0:
            is_prime = False
            break  # No need to keep looking
        prime_index += 1
    if is_prime:
        primes.append(i)
end = time.perf_counter()

print(len(primes))
print( f'Processing time: {end - start}')

The new processing time is reduced to 1.45 sec.

Memory requirements

For the memory analysis we will reduce the range of test values down to 542. That will give us 100 primes.
The total memory requirements for this code are as follows:

upper_limit: 32 bytes
primes: Initially 96 bytes and will grow
i: 32 bytes and while i will change, its size will not
root: 32 bytes
prime_index: 32 bytes
is_prime: 32 bytes

The total memory requirement initially will be 256 bytes. This is 96 bytes for the list of primes and 160 bytes for everything else. The only object that will grow will be the list of primes. Once it has 100 primes in it, it will take up a total of 4,120 bytes. That makes the total memory requirement for the entire app to run is 4,280 bytes.

Time requirements

Trial division runs in O(N²) time. This can be seen in the graph below.

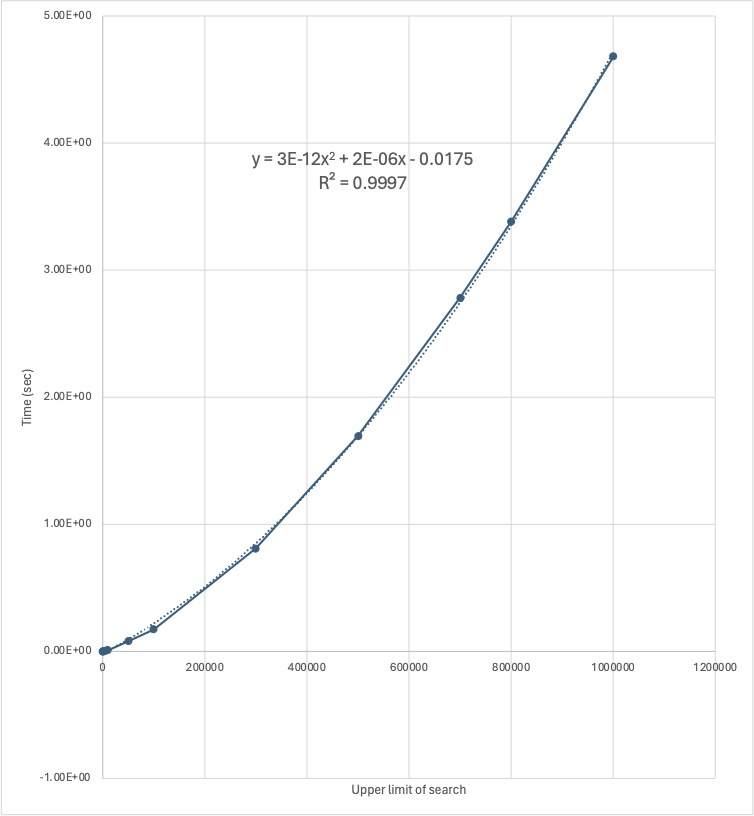
The x² term is very small and does not really take effect until N gets very large. For values of N below 100,000 the relationship between N and t is almost linear.

Last modified: 25 May 2024